a monadic type system adds a type that says “this term is impure”
at least, that’s a simple way of doing this
we’re also going to add as a suspended effectful computation, i.e. you can make an impure computation pure by just not running it
and we’re going to extend our typing judgements to be mutually recursive: split into pure typing judgements and effectful type judgements:
pure terms:
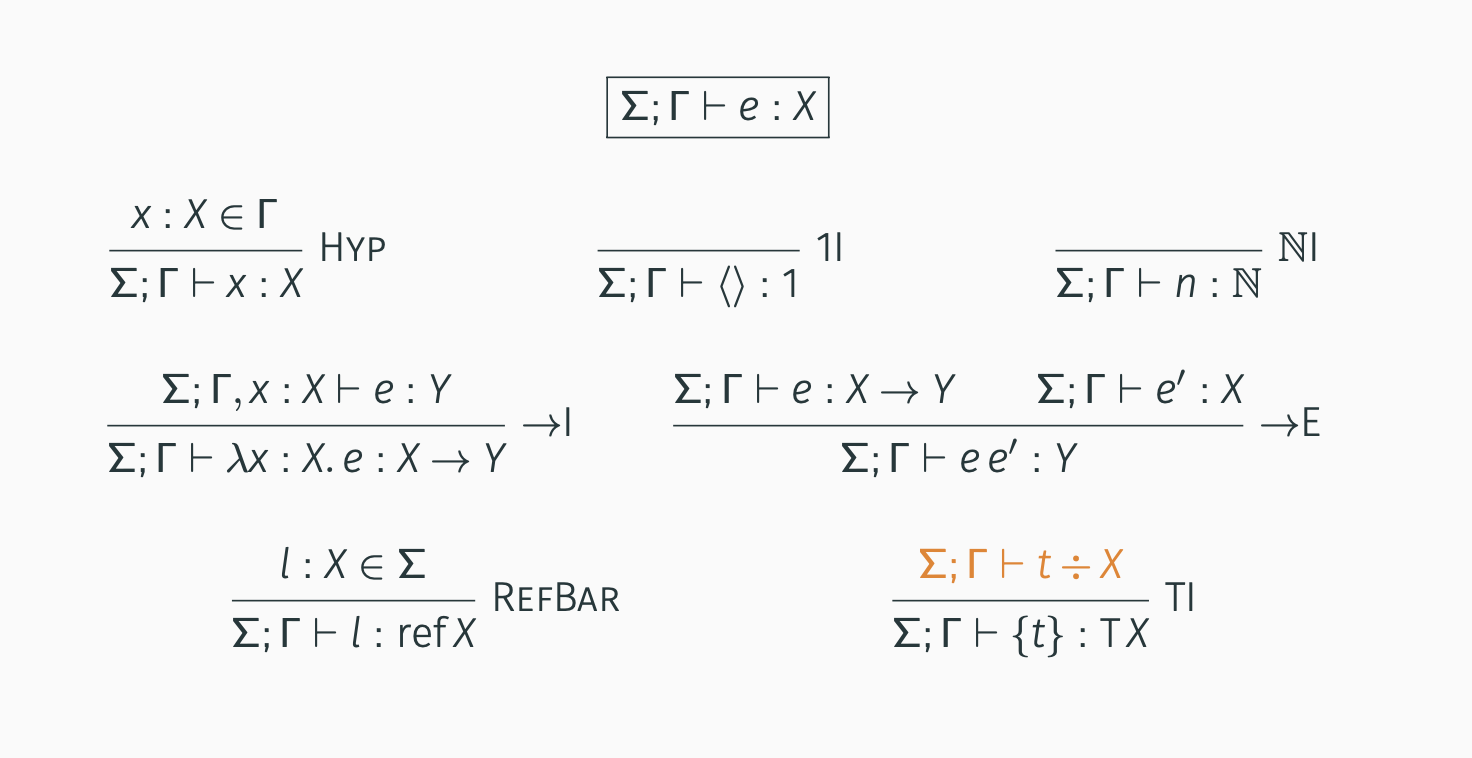
effect terms:

so we’re introduction and elimination rules for the monad
and notably the fact that doesn’t have an effect means that we can promote pure computations to impure computations. monadic type systems are a conservative approximation, they assume that everything with the monad type is impure, and so anything that relies on that computation is impure, even if it’s not. this means you can’t encapsulate exceptions — the type system thinks you might raise an exception since your inner function raises one, even though you’ve caught all possible exceptions.
so now all our proofs are mutual inductions: we prove exchange and weakening mutually between pure and impure.
but, in fact, you can prove the pure versions of progress and preservations without mutually recursing, since is a value, so impure computations are never evaluated when evaluating pure terms.