cat theory exercise sheet 2

coproducts

Distributive categories: A category $\mathbf{C}$ is distributive if it has all binary products and binary coproducts, and for all $X,Y,Z\in \text{obj }\mathbf{C}$, the unique morphism ${\delta }_{X,Y,Z}:(X\times Y)+(X\times Z)\to X\times (Y+Z)$ that makes commute is an isomorphism.

• Using the usual product and coproduct constructs in $\mathbf{Set}$, show that it is distributive.
• Give, with justification, an example of a category with binary products and coproducts that is not distributive.
• If $\mathbf{C}$ is a distributive category and $0$ is an initial object in $\mathbf{C}$, prove that for all $X\in \text{obj }\mathbf{C}$, the unique morphism $0\to X\times 0$ is an isomorphism.

Start with the last one, which is the most interesting.

Since $0$ is an initial object, we have a unique morphism $[]:0\to X\times 0$. We also have ${\pi }_2:X\times 0\to 0$. Now take arbitrary object $Y$, and take two arrows $f,g:X\times 0\to Y$. We know at least one, which we’ve shown in the diagram below $g=[{]}_Y\circ {\pi }_2$. We’ll show that this is in fact unique, which lets us show that $X\times 0$ is an initial object in $\mathbf{C}$, and hence isomorphic to $0$.

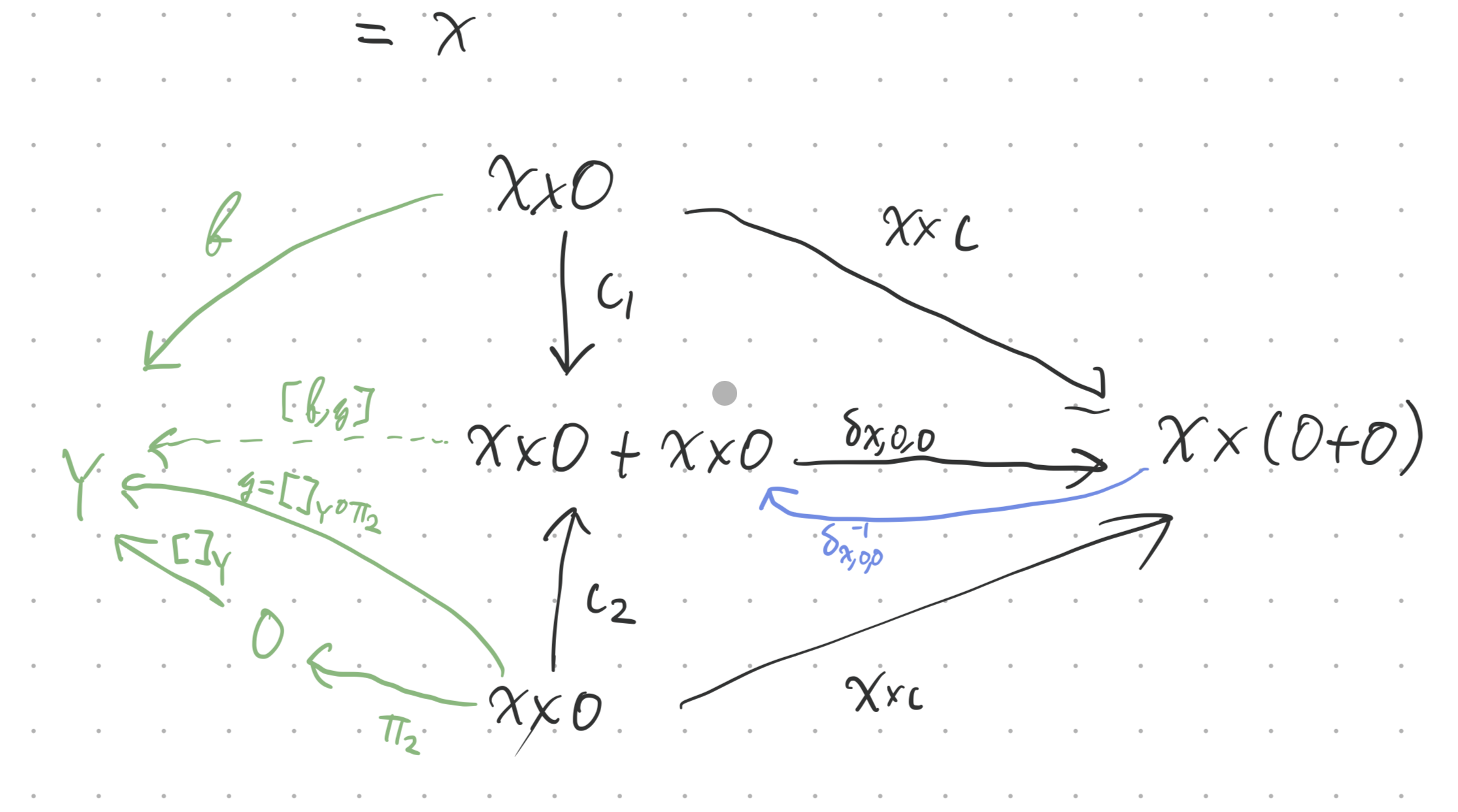
We know $[f,g]$. If we can show ${\iota }_1={\iota }_2$, then we’ll have $f=[f,g]\circ {\iota }_1=[f,g]\circ {\iota }_2=g$, and we’ll be done. So it suffices to show ${\iota }_1={\iota }_2$. Let’s zoom in:

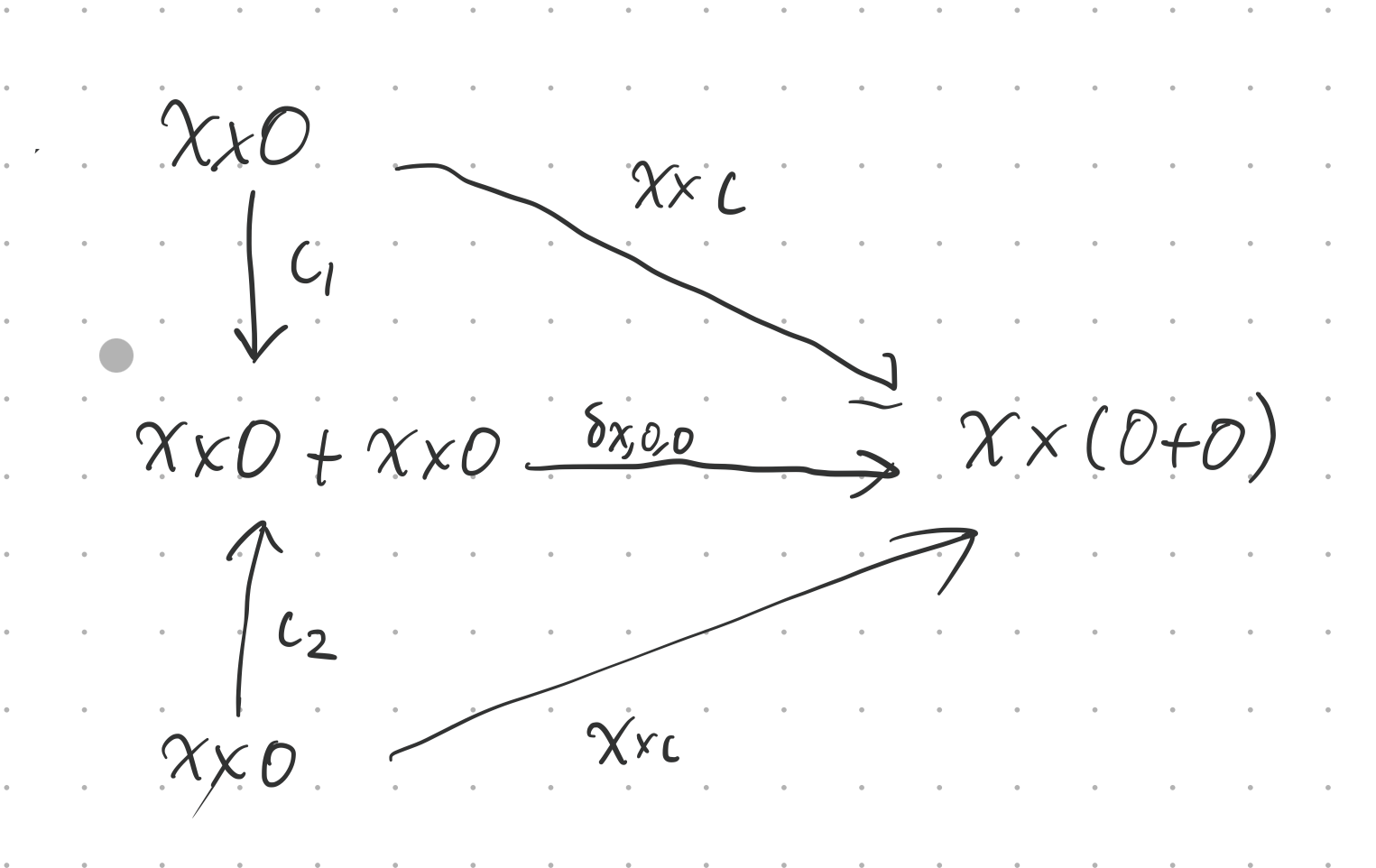
The two injections $0\to 0+0$ are equal, since $0$ is initial (so arrows out of it are unique). ${\delta }_{X,0,0}$ is an isomorphism by distributivity.

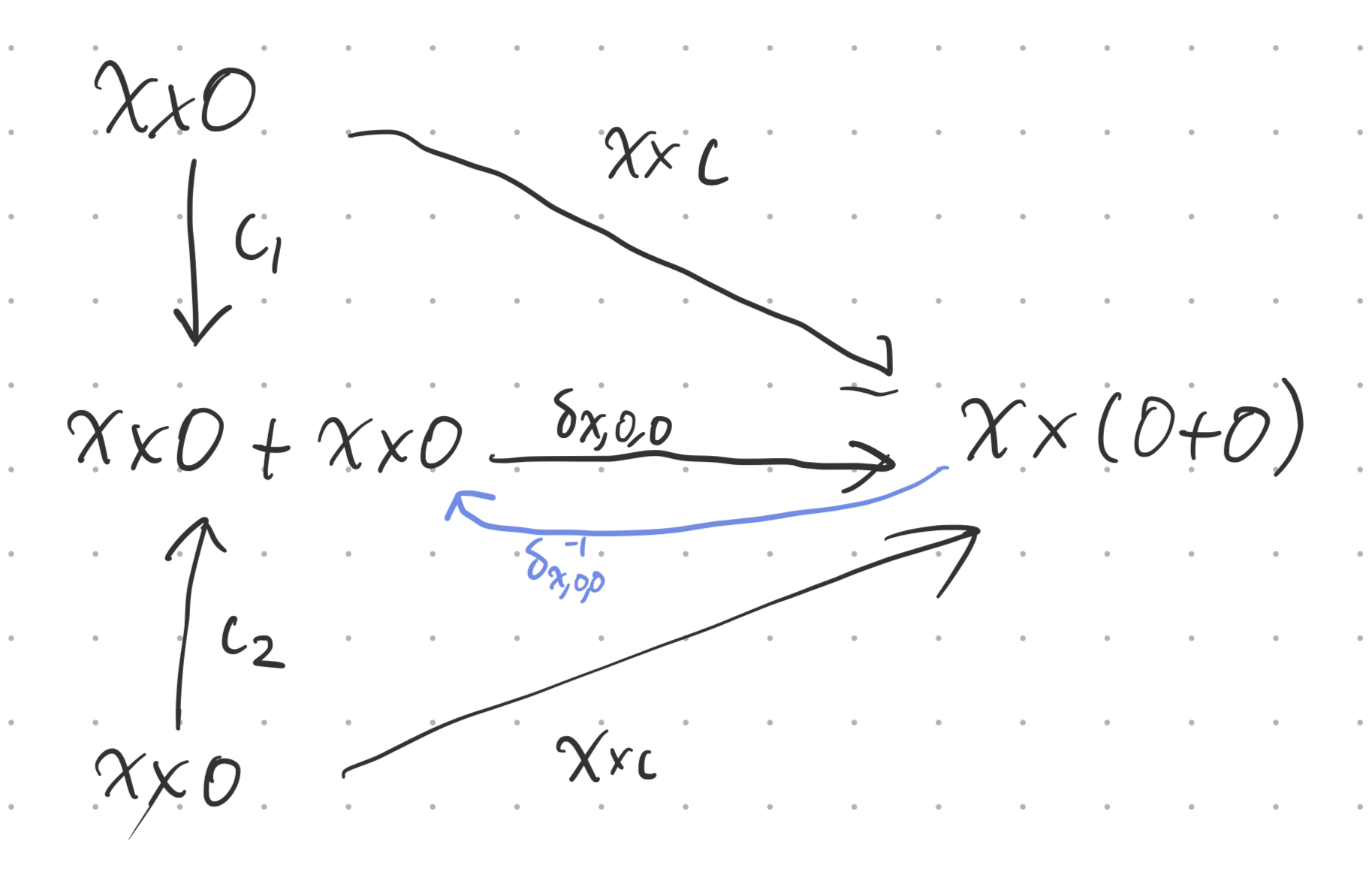
Since ${\iota }_1$ is the unique injection, we have that ${\delta }_{X,0,0}^{-1}\circ (X\times \iota )={\iota }_1$, and symmetrically for ${\iota }_2$, so ${\iota }_1={\iota }_2$, and so we’re done.